Congruent Triangles
Congruent triangles are triangles that have the same size and shape. This means that the corresponding sides are equal and the corresponding angles are equal.
In the above diagrams, the corresponding sides are a and d; b and e ; c and f.
The corresponding angles are x and s; y and t; z and u.
How to tell if triangles are congruent?
We can tell whether two triangles are congruent without testing all the sides and all the angles of the two triangles. There are four rules to check for congruent triangles. They are called the SSS rule, SAS rule, ASA rule and AAS rule. There is also another rule for right triangles called the Hypotenuse Leg rule. As long as one of the rules is true, it is sufficient to prove that the two triangles are congruent.
SSS Rule
The Side-Side-Side (SSS) rule states that
If three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent.
SAS Rule
The Side-Angle-Side (SAS) rule states that
If two sides and the included angle of one triangle are equal to two sides and included angle of another triangle, then the triangles are congruent.
An included angle is the angle formed by the two given sides.
Included Angle Non-included angle
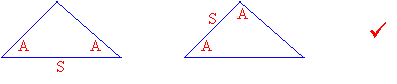
ASA Rule
The Angle-Side-Angle (ASA) Rule states that
If two angles and the included side of one triangle are equal to two angles and included side of another triangle, then the triangles are congruent.
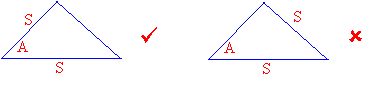
An included side is the side between the two given angles.
AAS Rule
The Angle-Angle-Side (AAS) Rule states that
If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle, then the triangles are congruent.
(This rule may sometimes be refered to as SAA).
For the ASA rule the given side must be included and for AAS rule the side given must not be included. The trick is we must use the same rule for both the triangles that we are comparing.
Compare AAS with AAS
Compare ASA with ASA



No comments:
Post a Comment