Sunday 24 November 2013

Trignometric Identites

Trignometric Identites You have seen quite a few trigonometric identities in the past few pages. It is convenient to have a summary of them for reference. These identities mostly refer to one angle denoted θ, but there are some that involve two angles, and for those, the two angles are denoted α and β.

The more important identities. You don’t have to know all the identities off the top of your head. But these you should.

	Defining relations for tangent, cotangent, secant, and cosecant in terms of sine and cosine.
	The Pythagorean formula for sines and cosines. This is probably the most important trig identity.
	Identities expressing trig functions in terms of their complements. There's not much to these. Each of the six trig functions is equal to its co-function evaluated at the complementary angle.
	Periodicity of trig functions. Sine, cosine, secant, and cosecant have period 2π while tangent and cotangent have period π.
	Identities for negative angles. Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions.
	Sum and difference formulas for sine and cosine.
	Double angle formulas for sine and cosine. Note that there are three forms for the double angle formula for cosine. You only need to know one, but be able to derive the other two from the Pythagorean formula.


The less important identities. You should know that there are these identities, but they are not as important as those mentioned above. They can all be derived from those above, but sometimes it takes a bit of work to do so.

	The Pythagorean formula for tangents and secants. There’s also one for cotangents and cosecants, but as cotangents and cosecants are rarely needed, it’s unnecessary.
	Identities expressing trig functions in terms of their supplements.
	Sum, difference, and double angle formulas for tangent.
	The half angle formulas. The ones for sine and cosine take the positive or negative square root depending on the quadrant of the angle θ/2. For example, if θ/2 is an acute angle, then the positive root would be used.

Truly obscure identities. These are just here for perversity. No, not really. They have some applications, but they’re usually narrow applications, and they could just as well be forgotten until needed.

	Product-sum identities. This group of identities allow you to change a sum or difference of sines or cosines into a product of sines and cosines.
	Product identities. Aside: weirdly enough, these product identities were used before logarithms were invented in order to perform multiplication. Here’s how you could use the second one. If you want to multiply x times y, use a table to look up the angle α whose cosine is x and the angle β whose cosine is y. Look up the cosines of the sum α + β. and the difference α – β. Average those two cosines. You get the product xy! Three table look-ups, and computing a sum, a difference, and an average rather than one multiplication. Tycho Brahe (1546–1601), among others, used this algorithm known as prosthaphaeresis.
	Triple angle formulas. You can easily reconstruct these from the addition and double angle formulas.
	More half-angle formulas. These describe the basic trig functions in terms of the tangent of half the angle. These are used in calculus for a particular kind of substitution in integrals sometimes called the Weierstrass t-substitution.

Congruent Triangles

Congruent triangles are triangles that have the same size and shape. This means that the corresponding sides are equal and the corresponding angles are equal.

In the above diagrams, the corresponding sides are a and d; b and e ; c and f.

The corresponding angles are x and s; y and t; z and u.

How to tell if triangles are congruent?

We can tell whether two triangles are congruent without testing all the sides and all the angles of the two triangles. There are four rules to check for congruent triangles. They are called the SSS rule, SAS rule, ASA rule and AAS rule. There is also another rule for right triangles called the Hypotenuse Leg rule. As long as one of the rules is true, it is sufficient to prove that the two triangles are congruent.

SSS Rule

The Side-Side-Side (SSS) rule states that

If three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent.

SAS Rule

The Side-Angle-Side (SAS) rule states that

If two sides and the included angle of one triangle are equal to two sides and included angle of another triangle, then the triangles are congruent.

An included angle is the angle formed by the two given sides.

Included Angle Non-included angle

ASA Rule

The Angle-Side-Angle (ASA) Rule states that

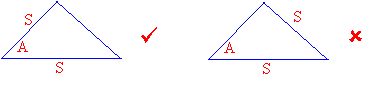
If two angles and the included side of one triangle are equal to two angles and included side of another triangle, then the triangles are congruent.

An included side is the side between the two given angles.

AAS Rule

The Angle-Angle-Side (AAS) Rule states that

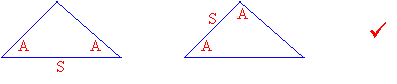
If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle, then the triangles are congruent.
(This rule may sometimes be refered to as SAA).

For the ASA rule the given side must be included and for AAS rule the side given must not be included. The trick is we must use the same rule for both the triangles that we are comparing.

Compare AAS with AAS

Compare ASA with ASA

Saturday 23 November 2013

Basic Rules of Algebra

Basic Rules Of Algebra

Basic Rules of Algebra

There are basic properties in math that apply to all real numbers. When working with variables in algebra, these properties still apply. We will apply most of the following properties to solve various Algebraic problems.

Algebraic Properties

Let a, b, and c be real numbers, variables, or algebraic expressions.

Commutative Property of Addition

We can add numbers in any order.

Commmutative Property of Multiplication

We can also multiply numbers in any order.

Associative Property of Addition

We can group numbers in a sum any way we want and get the same answer.

Associative Property of Multiplication

We can group numbers in a product any way we want and get the same answer.

Distributive Property

When we are adding and multiplying with a parenthesis, we can distribute the multiplication through the addition.

For an in depth discussion, see Distributive Property

Additive Identity Property

If we add 0 to any number, we will end up with the same number.

Multiplicative Identity Property

If we multiply 1 to any number, we will end up with the same number.

Additive Inverse Property

If we adda number by the opposite of itself, we will end up with 0.

Multiplicative Inverse Property

If we multiply a number by its reciprocal, we will end up with 1.

Keep in mind that subtraction is also considered addition, but with a negative number. Similarly, divison can be thought of as inverse multiplication, but with a restriction that the denominator cannot be equal to 0.